Model Training with Machine Learning

Welcome to Part 6 of our Data Science Primer. In this guide, we will take you step-by-step through the model training process. Since we’ve already done the hard part, actually fitting (a.k.a. training) our model will be fairly straightforward.

There are a few key techniques that we’ll discuss, and these have become widely-accepted best practices in the field. Again, this primer is meant to be a gentle introduction to data science and machine learning, so we won’t get into the nitty gritty yet. We have plenty of other tutorials for that.

How to Train ML Models

At last, it’s time to build our models! It might seem like it took us a while to get here, but professional data scientists actually spend the bulk of their time on the steps leading up to this one:

Exploring the data.
Cleaning the data.
Engineering new features.

Again, that’s because better data beats fancier algorithms.

In this guide, you’ll learn how to set up the entire modeling process to maximize performance while safeguarding against overfitting. We will swap algorithms in and out and automatically find the best parameters for each one.

Split Dataset

Let’s start with a crucial but sometimes overlooked step: Spending your data. Think of your data as a limited resource.

You can spend some of it to train your model (i.e. feed it to the algorithm).
You can spend some of it to evaluate (test) your model.
But you can’t reuse the same data for both!

If you evaluate your model on the same data you used to train it, your model could be very overfit and you wouldn’t even know! A model should be judged on its ability to predict new, unseen data.

Therefore, you should have separate training and test subsets of your dataset.

Training sets are used to fit and tune your models. Test sets are put aside as “unseen” data to evaluate your models.

You should always split your data before doing anything else. This is the best way to get reliable estimates of your models’ performance. After splitting your data, don’t touch your test set until you’re ready to choose your final model!

Comparing test vs. training performance allows us to avoid overfitting… If the model performs very well on the training data but poorly on the test data, then it’s overfit.

What are Hyperparameters?

So far, we’ve been casually talking about “tuning” models, but now it’s time to treat the topic more formally. When we talk of tuning models, we specifically mean tuning hyperparameters.

There are two types of parameters in machine learning algorithms. The key distinction is that model parameters can be learned directly from the training data while hyperparameters cannot.

Tuning Some Hyperparameters — “Don’t mind me. Just randomly pressing buttons carefully tuning parameters.”

Model parameters are learned attributes that define individual models. They can be learned directly from the training data.

e.g. regression coefficients
e.g. decision tree split locations

Hyperparameters express “higher-level” structural settings for algorithms. They are decided before fitting the model because they can’t be learned from the data.

e.g. strength of the penalty used in regularized regression
e.g. the number of trees to include in a random forest

What is Cross-Validation?

Next, it’s time to introduce a concept that will help us tune our models: cross-validation. Cross-validation is a method for getting a reliable estimate of model performance using only your training data.

There are several ways to cross-validate. The most common one, 10-fold cross-validation, breaks your training data into 10 equal parts (a.k.a. folds), essentially creating 10 miniature train/test splits.

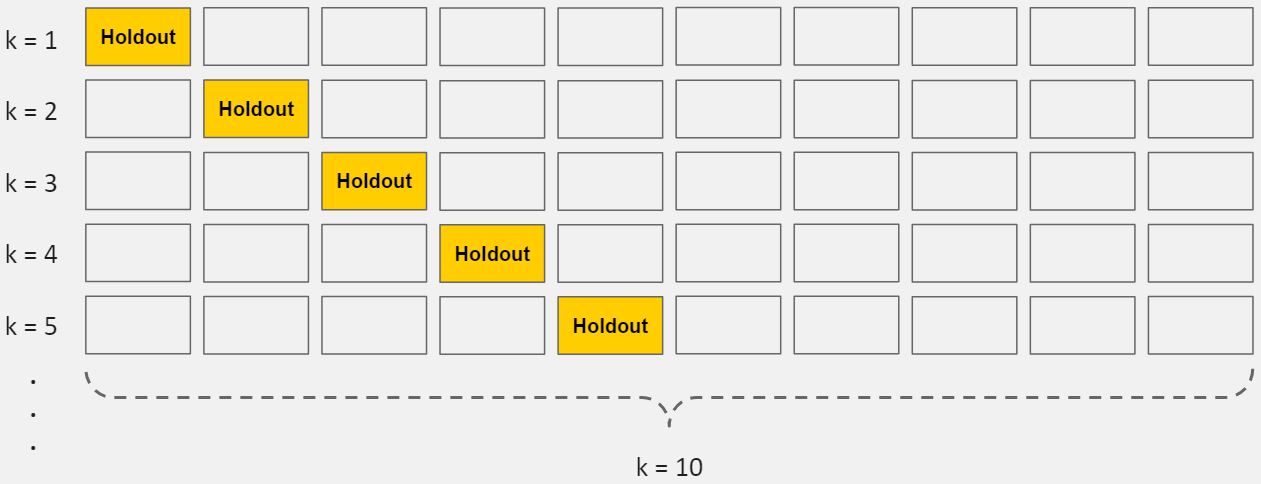
These are the steps for 10-fold cross-validation:

Split your data into 10 equal parts, or “folds”.
Train your model on 9 folds (e.g. the first 9 folds).
Evaluate it on the 1 remaining “hold-out” fold.
Perform steps (2) and (3) 10 times, each time holding out a different fold.
Average the performance across all 10 hold-out folds.

The average performance across the 10 hold-out folds is your final performance estimate, also called your cross-validated score. Because you created 10 mini train/test splits, this score is usually pretty reliable.

Fit and Tune Models

Now that we’ve split our dataset into training and test sets, and we’ve learned about hyperparameters and cross-validation, we’re ready fit and tune our models. Basically, all we need to do is perform the entire cross-validation loop detailed above on each set of hyperparameter values we’d like to try.

The high-level pseudo-code looks like this:

For each algorithm (i.e. regularized regression, random forest, etc.):

For each set of hyperparameter values to try:

Perform cross-validation using the training set.

Calculate cross-validated score.

At the end of this process, you will have a cross-validated score for each set of hyperparameter values… for each algorithm.

For example:

Then, we’ll pick the best set of hyperparameters within each algorithm.

For each algorithm:

Keep the set of hyperparameter values with best cross-validated score.

Re-train the algorithm on the entire training set (without cross-validation).

It’s kinda like the Hunger Games… each algorithm sends its own “representatives” (i.e. model trained on the best set of hyperparameter values) to the final selection.

Select Winning Model

By now, you’ll have one “best” model for each algorithm that has been tuned through cross-validation. Most importantly, you’ve only used the training data so far. Now it’s time to evaluate each model and pick the best one, Hunger Games style.

ML Hunger Games — “I volunteer as tribute!”

Because you’ve saved your test set as a truly unseen dataset, you can now use it get a reliable estimate of each models’ performance.

There are a variety of performance metrics you could choose from. We won’t spend too much time on them here, but in general:

For regression tasks, we recommend Mean Squared Error (MSE) or Mean Absolute Error (MAE). (Lower values are better)
For classification tasks, we recommend Area Under ROC Curve (AUROC). (Higher values are better)

The process is very straightforward:

For each of your models, make predictions on your test set.
Calculate performance metrics using those predictions and the “ground truth” target variable from the test set.

Finally, use these questions to help you pick the winning model:

Which model had the best performance on the test set? (performance)
Does it perform well across various performance metrics? (robustness)
Did it also have (one of) the best cross-validated scores from the training set? (consistency)
Does it solve the original business problem? (win condition)

That wraps it up for the Model Training step of the Machine Learning Workflow. To get more hands-on practice, we recommend checking out some of the additional resources below or join us in our Machine Learning Accelerator course.

More on Model Training

Read the rest of our Intro to Data Science here.